1208 Ways to Uncap NES Tetris
tetris, hacking ·In this post, we’ll construct a bunch of game genie codes that all do exactly the same thing. Along the way, we’ll look through the history all the ways that NES Tetris players view scores past one million points. This assumes a light level of comfort with programming (in particular concepts like hexadecimal and assembly), but all concepts should have an explanation or link attached.
Background
In the original NES Tetris, the highest possible score is 999,999; any points scored above it will never be shown on-screen. Reaching this threshold is known as a “maxout”, and in the decades since the game’s release, it’s become the most important benchmark in a player’s progression through the game. However, much higher scores would be attainable if the cap didn’t exist, so challenge-seeking players began looking for ways to track this.
The most straightforward solution is to take a video recording of a game and manually add the points scored past a maxout. This works, but is inconvenient and prone to errors. An easier solution, and the one that saw more popularity, was to use a Game Genie, a “cheat” device produced by Galoob.
By entering up to three codes — strings of 6 or 8 letters like AEPPOZ or SXVOKLAP — players could change the behavior of their games to, for example, gain invincibility or extra items. Though each code could only modify a single byte of the game’s ROM, this was still more than enough to cause drastic differences in gameplay. In our case, just one special GG lets us see scores past the maxout, and all we have to do is enter it once at the start of each session; way easier than all that math. Here’s what it looks like:
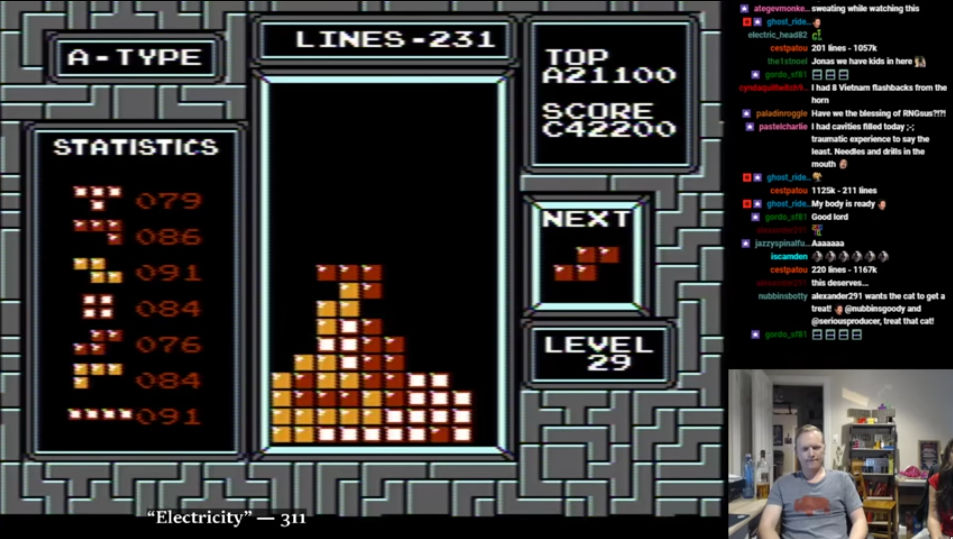
The result is a sort of pseudo-hexadecimal representation. Rather than adding a 7th digit to the left of the score, we simply increase the leading digit that already exists. In the spirit of hexadecimal, after 9 comes A, then B, and then so on. Thus, the score shown above is 1,242,200.
In the next couple of sections, we’ll investigate how we might be able to construct these codes. We’ll start with the first one that was discovered, ENEOOGEZ, and then move on to its improvement, XNEOOGEX, and see why it’s actually more correct. And then, of course, we’ll go completely crazy and find all the other thousand-plus codes.
How to Create ENEOOGEZ
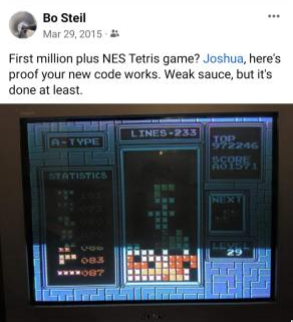
ENEOOGEZ was first discovered by Joshua Tolles and released on March 21st, 2015 (just in case, here’s a wayback link too). Within 8 days, Bo Steil used it to set the first documented score past one million points, as seen by this Facebook post that appears to be deleted now:
We’re gonna work our way up to understanding ENEOOGEZ, but first we need to understand the assembly that it modifies:
9C84: A5 55 LDA score+2 ; fetch the leading two digits of the score
9C86: 29 F0 AND #$F0 ; only consider the leading digit
9C88: C9 A0 CMP #$A0 ; if the digit is less than 0x0A,
9C8A: 90 08 BCC @noMaxout ; branch to @noMaxout
9C8C: A9 99 LDA #$99 ; otherwise, the score is over 1 million,
9C8E: 85 53 STA score+0 ; so we set all digits to 9
9C90: 85 54 STA score+1
9C92: 85 55 STA score+2
@noMaxout:
9C94: C6 A8 DEC generalCounter ; loop cleanup things, not important here
9C96: D0 9F BNE @addPointsLoopAlongside the raw assembly itself, there’s a lot of supplemental info. Each line of assembly starts with an address (e.g. 9C84:), corresponding to the raw memory location of the instruction. Next is the encoding of the instruction into bytes. Thus, memory location 0x9C84 contains the value 0xA5, while 0x9C8B contains 0x08. Finally, we have the instruction and its operand, which can be a hexadecimal number or a label with an optional offset. For example, score is used to represent 0x53, so score+2 represents 0x55. And anything past a semicolon is a comment.
There’s one more thing we need to know, and it’s about how NES Tetris keeps
track of the score. The game uses little-endian binary-coded decimal (or BCD), since this ends up being convenient when displaying the score on-screen. Thus, a score of 123456 would be stored as 0x56, 0x34, 0x12 in memory locations 0x53, 0x54, 0x55, respectively (note that each pair of digits is in hexadecimal. If you wanted, you could also represent the stored values as 86, 52, 18, but this makes less semantic sense).
However, while displaying the score is easier, adding points to it is harder. The game will try to add points like normal, but it has special logic to detect carries. For example, when adding 0x09 and 0x04, the first intermediate result will be 0x0D. Since D is not a decimal digit, we know there’s a carry, so this number gets converted to 0x13, which is the final result.
With that out of the way, let’s get to the code itself. Fundamentally, a game genie code is an obfuscation of two or three values: a memory address, a replacement data byte, and an optional compare byte, which is required to match (this is used as a sanity check, or for games that employ bank switching, at which point one address could point to several code locations). Including the compare byte results in an 8 letter code, and excluding it results in a 6 letter code. If you’re curious, you can find the technical details for its algorithm here, along with a calculator that can convert these parameters to codes, and vice versa. The map from code to parameters is unique, but the reverse is not true; each valid set of parameters actually corresponds to two game genie codes.
ENEOOGEZ specifies an address of 0x9C89 with replacement data 0xF0, using a compare value of 0xA0. As a sanity check, if we look at the code above, we can see that address 0x9C89 does currently contain 0xA0. Next, we’ll look at the top half in more detail:
9C84: A5 55 LDA score+2 ; fetch the leading two digits of the score
9C86: 29 F0 AND #$F0 ; strip out the lower digit
9C88: C9 A0 CMP #$A0 ; if the digit is less than 0x0A,
9C8A: 90 08 BCC @noMaxout ; branch to @noMaxoutHypothetically, let’s say our score was 995,001, and we’ve just added 9,000 points.1 The resulting score is 1,004,001, but how is that stored in three bytes? Well, remember when we talked about adding points with BCD numbers? I mentioned that there’s special logic to detect carries, but this doesn’t actually apply to the leading digit. Thus, score+2 will contain 0xA0 (and score+1 contains 0x40 and score+0 contains 0x01).
And now, I hope the CMP #$A0 makes sense: if the leading byte is above 0xA0, that means our score is over a million! Thus, we do not take the branch, and we instead run this block of code that manually sets the score to 999,999:
9C8C: A9 99 LDA #$99
9C8E: 85 53 STA score+0
9C90: 85 54 STA score+1
9C92: 85 55 STA score+2So this is how this bit of the normal game’s code works at a high level. Using ENEOOGEZ, however, first half of the segment looks like this:
9C84: A5 55 LDA score+2 ; fetch the leading two digits of the score
9C86: 29 F0 AND #$F0 ; strip out the lower digit
9C88: C9 F0 CMP #$F0 ; if the digit is less than 0x0F,
9C8A: 90 08 BCC @noMaxout ; branch to @noMaxoutWith the same scenario from earlier, we’re now comparing 0xA0 to 0xF0, and this time it’s less! Thus, we take the branch, and the score isn’t set to 999,999. Yay!
For basically the entire time ENEOOGEZ was used, it worked flawlessly. However, there’s a subtle problem with it. Try and think of a way that this code might not function the way we want; we’ll discuss the answer in the next section.
Improving to XNEOOGEX
Before we get to the gotcha, here’s a brief history of XNEOOGEX. It was created around July 11, 2019 by Kirby703. The earliest mention of it in the Classic Tetris Monthly discord dates December 14, 2019.2 Over a period of months, it gradually grew more popular because of its slight technical correctness over ENEOOGEZ, and also because it had lots of X’s which sounds cool i guess.
Some time later, a new trend towards XNAOOK was formed, which is the version of XNEOOGEX without the compare byte. For NES Tetris, 6 and 8 letter codes work exactly the same, and it takes less time to enter 6 letters than it does for 8, and enough people cared about the slight efficiency boost. An exact date for this is unclear; the earliest I can find is a message from Kibi Byte sent on pi day of 2020.
So, where does ENEOOGEZ go wrong? Well, let’s slightly modify our example from earlier and say we’re adding 9,000 points to a score of 1,499,501, which is stored using the bytes 0x01, 0x95, 0xE9. Going through the same motions, the highest byte of the score is 0xF0, so when this is compared to 0xF0 on line 0x9C88, we don’t get a “less than” result, and we don’t take the branch! The consequence of this is that we go from 1,499,501 to 999,999; definitely not ideal. At the time, nobody was capable of getting anywhere close to 1.5 million, so this didn’t really matter, but nowadays it’s been reached by dozens of people.
XNEOOGEX solves this by increasing the replacement byte to 0xFA. Since we always AND the high byte of the score with 0xF0, all possible results of this AND will be less than 0xFA, meaning the @noMaxout branch is always taken, and all is right with the world.
This behavior is particularly interesting when we cross from 1.5 million to 1.6 million. In this case, the highest byte actually wraps around back to 0x00 and beyond, so a score of exactly 1.6 million would be displayed as 000000. This is known as the “rollover,” and has become a milestone for the especially elite players.
Finding Codes
Now that we have a bit of practice with understanding game genie codes, let’s try and find some more of them! As a refresher, here’s the code segment that caps the score:
9C84: A5 55 LDA score+2 ; fetch the leading two digits of the score
9C86: 29 F0 AND #$F0 ; only consider the leading digit
9C88: C9 A0 CMP #$A0 ; if the digit is less than 0x0A,
9C8A: 90 08 BCC @noMaxout ; branch to @noMaxout
9C8C: A9 99 LDA #$99 ; otherwise, we have a score over 1 million,
9C8E: 85 53 STA score+0 ; so we set all digits to 9
9C90: 85 54 STA score+1
9C92: 85 55 STA score+2
@noMaxout:
9C94: C6 A8 DEC generalCounter ; loop cleanup things, not important here
9C96: D0 9F BNE @addPointsLoopIf you feel comfortable with the syntax, you might find it fun to try and figure out some codes for yourself. When you’re ready, we’ll get started.
All of the codes I found can be classified using one of three strategies, each targeting a specific address. When discussing each strategy, we’ll only talk about the address/data combinations (since we know the address, we also know the compare value). It turns out that there are four game genie codes for each address/data combination: two without including the compare value and two including the compare value. As such, we’re only gonna discuss the address/data combinations, and the grand totals will be saved for a later section.
Strategy 1: Raise the Compare Threshold
This is the strategy that contains XNEOOGEX, concerning the line at address 0x9C88. We saw that XNEOOGEX replaces the 0xF0 at address 0x9C89 with 0xFA. However, because we have an AND #$F0 right before, we can actually get away with anything from 0xF1 to 0xFF (since the AND always sets the lower nybble to 0) inclusive, for a total of 15 possibilities.
Strategy 2: Change the Compare Mask
Of couse, why worry about the effects of the AND mask when we could just change the mask itself? Here, we make it so the result of score+2 AND mask is always less than 0xA0, where mask is what our game genie code substitutes in. It turns out that this is possible exactly when mask is strictly less than 0xA0.
Fun bit of trivia: this isn’t the first time somebody’s used this strategy before. Meatfighter, known in the community for an article about the internals of NES Tetris (including this segment of code we’ve been discussing!), details the method (as well as the flaw with ENEOOGEZ) in this article. It was released on August 17, 2019, a bit after the discovery of XNEOOGEX, but well before its public debut. He changes the mask to 0x00, which corresponds to the game genie code AEEPNGEY.
In total, there are 0xA0 = 160 valid values for the mask, which need to be applied to address 0x9C87.
Strategy 3: Change the Compare Data
I think this strategy is the most fun. Like the previous strategy, we mess with the result of score+2 AND mask. However, instead of changing mask, we change score+2 instead! This corresponds to address 0x9C85.
NES Tetris uses a fairly small portion of its (already limited) memory. However, using this specific instruction, we’re only able to substitute score+2 with 255 other bytes. Of these, this list contains all addresses that are never accessed, a total of 102:
0x03, 0x04, 0x07, 0x08, 0x09, 0x0a, 0x0b, 0x0c, 0x0d, 0x0e,
0x0f, 0x10, 0x11, 0x12, 0x13, 0x16, 0x1b, 0x1c, 0x1d, 0x1e,
0x1f, 0x20, 0x21, 0x22, 0x23, 0x24, 0x25, 0x26, 0x27, 0x28,
0x29, 0x2a, 0x2b, 0x2c, 0x2d, 0x2e, 0x2f, 0x30, 0x31, 0x32,
0x35, 0x36, 0x37, 0x38, 0x39, 0x3a, 0x3b, 0x3c, 0x3d, 0x3e,
0x3f, 0x43, 0x5b, 0x5c, 0x5d, 0x5e, 0x5f, 0x63, 0x7b, 0x7c,
0x7d, 0x7e, 0x7f, 0x80, 0x81, 0x82, 0x83, 0x84, 0x85, 0x86,
0x87, 0x88, 0x89, 0x8a ,0x8b, 0x8c, 0x8d, 0x8e, 0x8f, 0x90,
0x91, 0x92, 0x93, 0x94, 0x95, 0x96, 0x97, 0x98, 0x99, 0x9a,
0x9b, 0x9c, 0x9d, 0x9e, 0x9f, 0xb4, 0xe5, 0xe8, 0xe9, 0xf0,
0xf9, 0xfa,
We could stop here, but there are also a number of addresses that are used, but their values are guaranteed to be small. These values are listed here, along with their labels according to this reference and brief explanations of why they work:
0x19: spawnID, which is bounded above by 0x12
0x33: verticalBlankingInterval, which is 0 or 1
0x34: unused_0E, which is always 0x0E for some reason
0x40: tetriminoX, which is bounded by the board width, 10
0x41: tetriminoY, which is bounded by the board height, or 20
0x42: currentPiece, which is an ID bounded above by 0x12. this is also set
to 0x13 during line clears for some reason, but that's still fine.
0x46: autorepeatX, an internal count that's always between 0 and 16
0x47: startLevel, bounded above by 19
0x48: playState, which is between 0x00 and 0x0B inclusive
0x4A: completedRow, which is bounded by the board height, or 20
0x4F: holdDownPoints, which is bounded by the board height, or 20
there's a glitch that can allow pushdown points to stack, but this can
only happen at the start of each game, meaning scores are still fine
0x50: low byte of lines, which is between 0x00 and 0x99 inclusive
0x53: low byte of score, which is between 0x00 and 0x99 inclusive
0x54: middle byte of score, which is between 0x00 and 0x99 inclusive
In addition, the bottom group has a “player 1” analogue for each value, which you get by adding 0x20 to each address.3 Thus, there are a total of 3 + 2*11=25 additional addresses.
It’s very likely that more of these work, but verifying them would require much more effort. As it is right now, 102 + 25 = 127 of the 256 possible addresses work, which I think is pretty good.
Totalling all possible cases, we get 4*(15 + 160 + 127) = 1208 possible game genie codes! In this next section, we’ll actually generate the codes, as well as figure out what to do with all of them.
Generating and Ranking Codes
With these strategies, I wrote this script to generate every code that fit one of these criterions. When running it, we can see it generates 1,148 total codes — exactly what we calculated earlier. It’s certainly possible that there are others out there, however (maybe you can find some of them!).
The script doesn’t just list out the codes, though. I was curious about ways to “rank” the codes, and a natural criterion is the amount of time it takes to enter each one, which I consider equivalent to the “length” of the code. For the game genie, letters are arranged in this order:
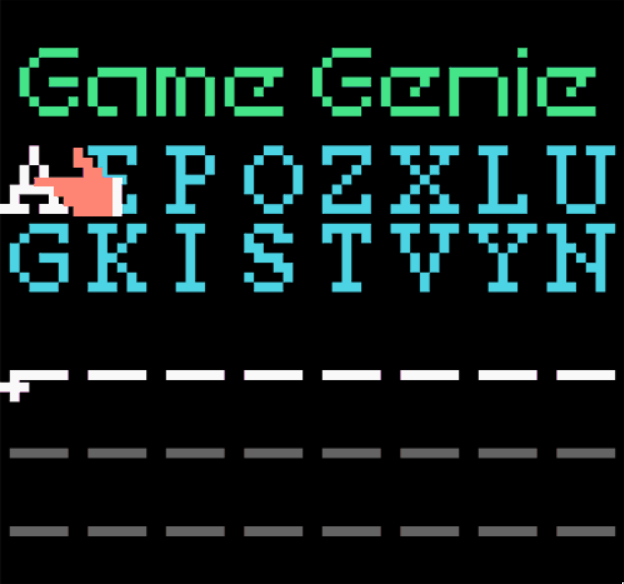
The cursor starts at A and is able to move horizontally and vertically at the same time, so the distance needed to enter any sequence of letters is the sum of all Chebyshev distances betwen adjacent letters, which is a needlessly fancy (read: fun) way of saying we take the max of the horizontal/vertical offset each time. For example, to enter the sequence AGPX, we travel a total distance of 1 + 2 + 3 = 6 units.
However, the Game Genie itself is not the only way to enter game genie codes. One alternative is the Everdrive N8, a flash cartridge which lets people play a practically unlimited number of games that they load on an SD card. Its code entry screen has this layout:
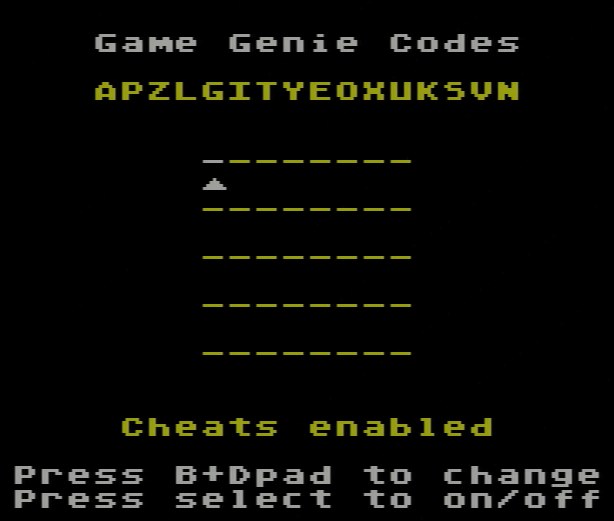
Unlike with the Game Genie, there is no “cursor memory,” and each letter is entered from the same state. This time, to enter AGPX, our total distance is 1 + 5 + 2 + 6 = 14, where we approach the X from the right side. It’s important to note that the Everdrive lets you load game genie codes from a text file, which sidesteps this whole process. However, that’s more boring so we’ll ignore that fact for now.
The script calculates this distance for every code, then finds the best and worst codes in terms of distance for both the Game Genie and the Everdrive. The Game Genie’s best codes are AEEPSK and EEEPSK, with distances of just 5. Looking at the grid, we see that both codes use the same circular motion around the left third of the screen. It’s hard to imagine that you can get more efficient than this. Between the two, I think AEEPSK is nicer because you don’t mash as much on the E. The worst codes are naturally 8 letters in length, and there are two: GUAPNGEN and GNAPNGEN, both with a distance of 36.
The best code for the Everdrive is ANAPNK, with a distance of 10. Amusingly, the worst possible code is ENEOOGEX (not actually the same as ENEOOGEZ), which has a distance of 50.
Finally, just for fun, here’s all 1208 codes:
ONAOOG ONEOOG ONAOOGEZ ONEOOGEZ XNAOOG XNEOOG XNAOOGEZ XNEOOGEZ
UNAOOG UNEOOG UNAOOGEZ UNEOOGEZ KNAOOG KNEOOG KNAOOGEZ KNEOOGEZ
SNAOOG SNEOOG SNAOOGEZ SNEOOGEZ VNAOOG VNEOOG VNAOOGEZ VNEOOGEZ
NNAOOG NNEOOG NNAOOGEZ NNEOOGEZ ENAOOK ENEOOK ENAOOGEX ENEOOGEX
ONAOOK ONEOOK ONAOOGEX ONEOOGEX XNAOOK XNEOOK XNAOOGEX XNEOOGEX
UNAOOK UNEOOK UNAOOGEX UNEOOGEX KNAOOK KNEOOK KNAOOGEX KNEOOGEX
SNAOOK SNEOOK SNAOOGEX SNEOOGEX VNAOOK VNEOOK VNAOOGEX VNEOOGEX
NNAOOK NNEOOK NNAOOGEX NNEOOGEX AEAPNG AEEPNG AEAPNGEY AEEPNGEY
PEAPNG PEEPNG PEAPNGEY PEEPNGEY ZEAPNG ZEEPNG ZEAPNGEY ZEEPNGEY
LEAPNG LEEPNG LEAPNGEY LEEPNGEY GEAPNG GEEPNG GEAPNGEY GEEPNGEY
IEAPNG IEEPNG IEAPNGEY IEEPNGEY TEAPNG TEEPNG TEAPNGEY TEEPNGEY
YEAPNG YEEPNG YEAPNGEY YEEPNGEY AEAPNK AEEPNK AEAPNGEN AEEPNGEN
PEAPNK PEEPNK PEAPNGEN PEEPNGEN ZEAPNK ZEEPNK ZEAPNGEN ZEEPNGEN
LEAPNK LEEPNK LEAPNGEN LEEPNGEN GEAPNK GEEPNK GEAPNGEN GEEPNGEN
IEAPNK IEEPNK IEAPNGEN IEEPNGEN TEAPNK TEEPNK TEAPNGEN TEEPNGEN
YEAPNK YEEPNK YEAPNGEN YEEPNGEN AOAPNG AOEPNG AOAPNGEY AOEPNGEY
POAPNG POEPNG POAPNGEY POEPNGEY ZOAPNG ZOEPNG ZOAPNGEY ZOEPNGEY
LOAPNG LOEPNG LOAPNGEY LOEPNGEY GOAPNG GOEPNG GOAPNGEY GOEPNGEY
IOAPNG IOEPNG IOAPNGEY IOEPNGEY TOAPNG TOEPNG TOAPNGEY TOEPNGEY
YOAPNG YOEPNG YOAPNGEY YOEPNGEY AOAPNK AOEPNK AOAPNGEN AOEPNGEN
POAPNK POEPNK POAPNGEN POEPNGEN ZOAPNK ZOEPNK ZOAPNGEN ZOEPNGEN
LOAPNK LOEPNK LOAPNGEN LOEPNGEN GOAPNK GOEPNK GOAPNGEN GOEPNGEN
IOAPNK IOEPNK IOAPNGEN IOEPNGEN TOAPNK TOEPNK TOAPNGEN TOEPNGEN
YOAPNK YOEPNK YOAPNGEN YOEPNGEN AXAPNG AXEPNG AXAPNGEY AXEPNGEY
PXAPNG PXEPNG PXAPNGEY PXEPNGEY ZXAPNG ZXEPNG ZXAPNGEY ZXEPNGEY
LXAPNG LXEPNG LXAPNGEY LXEPNGEY GXAPNG GXEPNG GXAPNGEY GXEPNGEY
IXAPNG IXEPNG IXAPNGEY IXEPNGEY TXAPNG TXEPNG TXAPNGEY TXEPNGEY
YXAPNG YXEPNG YXAPNGEY YXEPNGEY AXAPNK AXEPNK AXAPNGEN AXEPNGEN
PXAPNK PXEPNK PXAPNGEN PXEPNGEN ZXAPNK ZXEPNK ZXAPNGEN ZXEPNGEN
LXAPNK LXEPNK LXAPNGEN LXEPNGEN GXAPNK GXEPNK GXAPNGEN GXEPNGEN
IXAPNK IXEPNK IXAPNGEN IXEPNGEN TXAPNK TXEPNK TXAPNGEN TXEPNGEN
YXAPNK YXEPNK YXAPNGEN YXEPNGEN AUAPNG AUEPNG AUAPNGEY AUEPNGEY
PUAPNG PUEPNG PUAPNGEY PUEPNGEY ZUAPNG ZUEPNG ZUAPNGEY ZUEPNGEY
LUAPNG LUEPNG LUAPNGEY LUEPNGEY GUAPNG GUEPNG GUAPNGEY GUEPNGEY
IUAPNG IUEPNG IUAPNGEY IUEPNGEY TUAPNG TUEPNG TUAPNGEY TUEPNGEY
YUAPNG YUEPNG YUAPNGEY YUEPNGEY AUAPNK AUEPNK AUAPNGEN AUEPNGEN
PUAPNK PUEPNK PUAPNGEN PUEPNGEN ZUAPNK ZUEPNK ZUAPNGEN ZUEPNGEN
LUAPNK LUEPNK LUAPNGEN LUEPNGEN GUAPNK GUEPNK GUAPNGEN GUEPNGEN
IUAPNK IUEPNK IUAPNGEN IUEPNGEN TUAPNK TUEPNK TUAPNGEN TUEPNGEN
YUAPNK YUEPNK YUAPNGEN YUEPNGEN AKAPNG AKEPNG AKAPNGEY AKEPNGEY
PKAPNG PKEPNG PKAPNGEY PKEPNGEY ZKAPNG ZKEPNG ZKAPNGEY ZKEPNGEY
LKAPNG LKEPNG LKAPNGEY LKEPNGEY GKAPNG GKEPNG GKAPNGEY GKEPNGEY
IKAPNG IKEPNG IKAPNGEY IKEPNGEY TKAPNG TKEPNG TKAPNGEY TKEPNGEY
YKAPNG YKEPNG YKAPNGEY YKEPNGEY AKAPNK AKEPNK AKAPNGEN AKEPNGEN
PKAPNK PKEPNK PKAPNGEN PKEPNGEN ZKAPNK ZKEPNK ZKAPNGEN ZKEPNGEN
LKAPNK LKEPNK LKAPNGEN LKEPNGEN GKAPNK GKEPNK GKAPNGEN GKEPNGEN
IKAPNK IKEPNK IKAPNGEN IKEPNGEN TKAPNK TKEPNK TKAPNGEN TKEPNGEN
YKAPNK YKEPNK YKAPNGEN YKEPNGEN ASAPNG ASEPNG ASAPNGEY ASEPNGEY
PSAPNG PSEPNG PSAPNGEY PSEPNGEY ZSAPNG ZSEPNG ZSAPNGEY ZSEPNGEY
LSAPNG LSEPNG LSAPNGEY LSEPNGEY GSAPNG GSEPNG GSAPNGEY GSEPNGEY
ISAPNG ISEPNG ISAPNGEY ISEPNGEY TSAPNG TSEPNG TSAPNGEY TSEPNGEY
YSAPNG YSEPNG YSAPNGEY YSEPNGEY ASAPNK ASEPNK ASAPNGEN ASEPNGEN
PSAPNK PSEPNK PSAPNGEN PSEPNGEN ZSAPNK ZSEPNK ZSAPNGEN ZSEPNGEN
LSAPNK LSEPNK LSAPNGEN LSEPNGEN GSAPNK GSEPNK GSAPNGEN GSEPNGEN
ISAPNK ISEPNK ISAPNGEN ISEPNGEN TSAPNK TSEPNK TSAPNGEN TSEPNGEN
YSAPNK YSEPNK YSAPNGEN YSEPNGEN AVAPNG AVEPNG AVAPNGEY AVEPNGEY
PVAPNG PVEPNG PVAPNGEY PVEPNGEY ZVAPNG ZVEPNG ZVAPNGEY ZVEPNGEY
LVAPNG LVEPNG LVAPNGEY LVEPNGEY GVAPNG GVEPNG GVAPNGEY GVEPNGEY
IVAPNG IVEPNG IVAPNGEY IVEPNGEY TVAPNG TVEPNG TVAPNGEY TVEPNGEY
YVAPNG YVEPNG YVAPNGEY YVEPNGEY AVAPNK AVEPNK AVAPNGEN AVEPNGEN
PVAPNK PVEPNK PVAPNGEN PVEPNGEN ZVAPNK ZVEPNK ZVAPNGEN ZVEPNGEN
LVAPNK LVEPNK LVAPNGEN LVEPNGEN GVAPNK GVEPNK GVAPNGEN GVEPNGEN
IVAPNK IVEPNK IVAPNGEN IVEPNGEN TVAPNK TVEPNK TVAPNGEN TVEPNGEN
YVAPNK YVEPNK YVAPNGEN YVEPNGEN ANAPNG ANEPNG ANAPNGEY ANEPNGEY
PNAPNG PNEPNG PNAPNGEY PNEPNGEY ZNAPNG ZNEPNG ZNAPNGEY ZNEPNGEY
LNAPNG LNEPNG LNAPNGEY LNEPNGEY GNAPNG GNEPNG GNAPNGEY GNEPNGEY
INAPNG INEPNG INAPNGEY INEPNGEY TNAPNG TNEPNG TNAPNGEY TNEPNGEY
YNAPNG YNEPNG YNAPNGEY YNEPNGEY ANAPNK ANEPNK ANAPNGEN ANEPNGEN
PNAPNK PNEPNK PNAPNGEN PNEPNGEN ZNAPNK ZNEPNK ZNAPNGEN ZNEPNGEN
LNAPNK LNEPNK LNAPNGEN LNEPNGEN GNAPNK GNEPNK GNAPNGEN GNEPNGEN
INAPNK INEPNK INAPNGEN INEPNGEN TNAPNK TNEPNK TNAPNGEN TNEPNGEN
YNAPNK YNEPNK YNAPNGEN YNEPNGEN EEAPNG EEEPNG EEAPNGEY EEEPNGEY
OEAPNG OEEPNG OEAPNGEY OEEPNGEY XEAPNG XEEPNG XEAPNGEY XEEPNGEY
UEAPNG UEEPNG UEAPNGEY UEEPNGEY KEAPNG KEEPNG KEAPNGEY KEEPNGEY
SEAPNG SEEPNG SEAPNGEY SEEPNGEY VEAPNG VEEPNG VEAPNGEY VEEPNGEY
NEAPNG NEEPNG NEAPNGEY NEEPNGEY EEAPNK EEEPNK EEAPNGEN EEEPNGEN
OEAPNK OEEPNK OEAPNGEN OEEPNGEN XEAPNK XEEPNK XEAPNGEN XEEPNGEN
UEAPNK UEEPNK UEAPNGEN UEEPNGEN KEAPNK KEEPNK KEAPNGEN KEEPNGEN
SEAPNK SEEPNK SEAPNGEN SEEPNGEN VEAPNK VEEPNK VEAPNGEN VEEPNGEN
NEAPNK NEEPNK NEAPNGEN NEEPNGEN EOAPNG EOEPNG EOAPNGEY EOEPNGEY
OOAPNG OOEPNG OOAPNGEY OOEPNGEY XOAPNG XOEPNG XOAPNGEY XOEPNGEY
UOAPNG UOEPNG UOAPNGEY UOEPNGEY KOAPNG KOEPNG KOAPNGEY KOEPNGEY
SOAPNG SOEPNG SOAPNGEY SOEPNGEY VOAPNG VOEPNG VOAPNGEY VOEPNGEY
NOAPNG NOEPNG NOAPNGEY NOEPNGEY EOAPNK EOEPNK EOAPNGEN EOEPNGEN
OOAPNK OOEPNK OOAPNGEN OOEPNGEN XOAPNK XOEPNK XOAPNGEN XOEPNGEN
UOAPNK UOEPNK UOAPNGEN UOEPNGEN KOAPNK KOEPNK KOAPNGEN KOEPNGEN
SOAPNK SOEPNK SOAPNGEN SOEPNGEN VOAPNK VOEPNK VOAPNGEN VOEPNGEN
NOAPNK NOEPNK NOAPNGEN NOEPNGEN LEAPSG LEEPSG LEAPSGII LEEPSGII
GEAPSG GEEPSG GEAPSGII GEEPSGII YEAPSG YEEPSG YEAPSGII YEEPSGII
AEAPSK AEEPSK AEAPSGIS AEEPSGIS PEAPSK PEEPSK PEAPSGIS PEEPSGIS
ZEAPSK ZEEPSK ZEAPSGIS ZEEPSGIS LEAPSK LEEPSK LEAPSGIS LEEPSGIS
GEAPSK GEEPSK GEAPSGIS GEEPSGIS IEAPSK IEEPSK IEAPSGIS IEEPSGIS
TEAPSK TEEPSK TEAPSGIS TEEPSGIS YEAPSK YEEPSK YEAPSGIS YEEPSGIS
AOAPSG AOEPSG AOAPSGII AOEPSGII POAPSG POEPSG POAPSGII POEPSGII
ZOAPSG ZOEPSG ZOAPSGII ZOEPSGII LOAPSG LOEPSG LOAPSGII LOEPSGII
TOAPSG TOEPSG TOAPSGII TOEPSGII LOAPSK LOEPSK LOAPSGIS LOEPSGIS
GOAPSK GOEPSK GOAPSGIS GOEPSGIS IOAPSK IOEPSK IOAPSGIS IOEPSGIS
TOAPSK TOEPSK TOAPSGIS TOEPSGIS YOAPSK YOEPSK YOAPSGIS YOEPSGIS
AXAPSG AXEPSG AXAPSGII AXEPSGII PXAPSG PXEPSG PXAPSGII PXEPSGII
ZXAPSG ZXEPSG ZXAPSGII ZXEPSGII LXAPSG LXEPSG LXAPSGII LXEPSGII
GXAPSG GXEPSG GXAPSGII GXEPSGII IXAPSG IXEPSG IXAPSGII IXEPSGII
TXAPSG TXEPSG TXAPSGII TXEPSGII YXAPSG YXEPSG YXAPSGII YXEPSGII
AXAPSK AXEPSK AXAPSGIS AXEPSGIS PXAPSK PXEPSK PXAPSGIS PXEPSGIS
ZXAPSK ZXEPSK ZXAPSGIS ZXEPSGIS LXAPSK LXEPSK LXAPSGIS LXEPSGIS
GXAPSK GXEPSK GXAPSGIS GXEPSGIS IXAPSK IXEPSK IXAPSGIS IXEPSGIS
TXAPSK TXEPSK TXAPSGIS TXEPSGIS YXAPSK YXEPSK YXAPSGIS YXEPSGIS
AUAPSG AUEPSG AUAPSGII AUEPSGII PUAPSG PUEPSG PUAPSGII PUEPSGII
ZUAPSG ZUEPSG ZUAPSGII ZUEPSGII IUAPSG IUEPSG IUAPSGII IUEPSGII
TUAPSG TUEPSG TUAPSGII TUEPSGII YUAPSG YUEPSG YUAPSGII YUEPSGII
AUAPSK AUEPSK AUAPSGIS AUEPSGIS PUAPSK PUEPSK PUAPSGIS PUEPSGIS
ZUAPSK ZUEPSK ZUAPSGIS ZUEPSGIS LUAPSK LUEPSK LUAPSGIS LUEPSGIS
GUAPSK GUEPSK GUAPSGIS GUEPSGIS IUAPSK IUEPSK IUAPSGIS IUEPSGIS
TUAPSK TUEPSK TUAPSGIS TUEPSGIS YUAPSK YUEPSK YUAPSGIS YUEPSGIS
LKAPSG LKEPSG LKAPSGII LKEPSGII LSAPSK LSEPSK LSAPSGIS LSEPSGIS
GSAPSK GSEPSK GSAPSGIS GSEPSGIS ISAPSK ISEPSK ISAPSGIS ISEPSGIS
TSAPSK TSEPSK TSAPSGIS TSEPSGIS YSAPSK YSEPSK YSAPSGIS YSEPSGIS
LVAPSG LVEPSG LVAPSGII LVEPSGII LNAPSK LNEPSK LNAPSGIS LNEPSGIS
GNAPSK GNEPSK GNAPSGIS GNEPSGIS INAPSK INEPSK INAPSGIS INEPSGIS
TNAPSK TNEPSK TNAPSGIS TNEPSGIS YNAPSK YNEPSK YNAPSGIS YNEPSGIS
EEAPSG EEEPSG EEAPSGII EEEPSGII OEAPSG OEEPSG OEAPSGII OEEPSGII
XEAPSG XEEPSG XEAPSGII XEEPSGII UEAPSG UEEPSG UEAPSGII UEEPSGII
KEAPSG KEEPSG KEAPSGII KEEPSGII SEAPSG SEEPSG SEAPSGII SEEPSGII
VEAPSG VEEPSG VEAPSGII VEEPSGII NEAPSG NEEPSG NEAPSGII NEEPSGII
EEAPSK EEEPSK EEAPSGIS EEEPSGIS OEAPSK OEEPSK OEAPSGIS OEEPSGIS
XEAPSK XEEPSK XEAPSGIS XEEPSGIS UEAPSK UEEPSK UEAPSGIS UEEPSGIS
KEAPSK KEEPSK KEAPSGIS KEEPSGIS SEAPSK SEEPSK SEAPSGIS SEEPSGIS
VEAPSK VEEPSK VEAPSGIS VEEPSGIS NEAPSK NEEPSK NEAPSGIS NEEPSGIS
EOAPSG EOEPSG EOAPSGII EOEPSGII OOAPSG OOEPSG OOAPSGII OOEPSGII
XOAPSG XOEPSG XOAPSGII XOEPSGII UOAPSG UOEPSG UOAPSGII UOEPSGII
KOAPSG KOEPSG KOAPSGII KOEPSGII SOAPSG SOEPSG SOAPSGII SOEPSGII
VOAPSG VOEPSG VOAPSGII VOEPSGII NOAPSG NOEPSG NOAPSGII NOEPSGII
EOAPSK EOEPSK EOAPSGIS EOEPSGIS OOAPSK OOEPSK OOAPSGIS OOEPSGIS
XOAPSK XOEPSK XOAPSGIS XOEPSGIS UOAPSK UOEPSK UOAPSGIS UOEPSGIS
KOAPSK KOEPSK KOAPSGIS KOEPSGIS SOAPSK SOEPSK SOAPSGIS SOEPSGIS
VOAPSK VOEPSK VOAPSGIS VOEPSGIS NOAPSK NOEPSK NOAPSGIS NOEPSGIS
KUAPSG KUEPSG KUAPSGII KUEPSGII SVAPSG SVEPSG SVAPSGII SVEPSGII
EVAPSK EVEPSK EVAPSGIS EVEPSGIS OVAPSK OVEPSK OVAPSGIS OVEPSGIS
ENAPSG ENEPSG ENAPSGII ENEPSGII ONAPSK ONEPSK ONAPSGIS ONEPSGIS
XNAPSK XNEPSK XNAPSGIS XNEPSGIS POAPSK POEPSK POAPSGIS POEPSGIS
LUAPSG LUEPSG LUAPSGII LUEPSGII GUAPSG GUEPSG GUAPSGII GUEPSGII
AKAPSG AKEPSG AKAPSGII AKEPSGII PKAPSG PKEPSG PKAPSGII PKEPSGII
ZKAPSG ZKEPSG ZKAPSGII ZKEPSGII TKAPSG TKEPSG TKAPSGII TKEPSGII
YKAPSG YKEPSG YKAPSGII YKEPSGII AKAPSK AKEPSK AKAPSGIS AKEPSGIS
ZKAPSK ZKEPSK ZKAPSGIS ZKEPSGIS YKAPSK YKEPSK YKAPSGIS YKEPSGIS
ASAPSG ASEPSG ASAPSGII ASEPSGII LSAPSG LSEPSG LSAPSGII LSEPSGII
GSAPSG GSEPSG GSAPSGII GSEPSGII AVAPSG AVEPSG AVAPSGII AVEPSGII
PVAPSG PVEPSG PVAPSGII PVEPSGII ZVAPSG ZVEPSG ZVAPSGII ZVEPSGII
TVAPSG TVEPSG TVAPSGII TVEPSGII YVAPSG YVEPSG YVAPSGII YVEPSGII
AVAPSK AVEPSK AVAPSGIS AVEPSGIS ZVAPSK ZVEPSK ZVAPSGIS ZVEPSGIS
YVAPSK YVEPSK YVAPSGIS YVEPSGIS ANAPSG ANEPSG ANAPSGII ANEPSGII
LNAPSG LNEPSG LNAPSGII LNEPSGII GNAPSG GNEPSG GNAPSGII GNEPSGII
Notice that this list doesn’t contain ENEOOGEZ. After all, it’s not always correct.
Conclusion
Nowadays, game genie codes aren’t really used to uncap scores. Currently, a romhack called Tetris Gym provides several practice modes and quality-of-life improvements, one of which is uncapping the score by default. With Gym, you don’t even need to enter a code to play with uncapped score, and as its popularity grew, the use for XNAOOK faded.
But at the same time, I believe the spirit of game genie codes live on as an art. In some sense, one can expect that anything is possible with a romhack, where you can change any number of bytes. But getting the same effects while changing only three? You might be surprised with what kinds of features are possible: we can enable 2 player mode (ZAUAPPPA), make pieces invisible (OXYOUO VNIPZN VNTPYN), and even implement hard drop (SZTAVO PAGENP). And I think exercises like this, doing a basic task like uncapping the score in an excessively overkill way, are another reflection of this art.
In summary, we should all ditch XNAOOK and use AEEPSK instead :D.
Edit 8/24/2023: Added footnote about the more complex history of XNEOOGEX, as communicated by Kirby703.
Also, received some corrections and suggestions from maya and Kitaru. In particular, maya reminded me that player 2 variables are never written to! This bumps the total from 1148 to 1208.
Notes
-
This is a gross (and incorrect) oversimplification of how adding points actually works, but that’s not really important here. ↩
-
There’s actually a couple of earlier messages, but these seem to be retroactively edited. Also, the code was allegedly mentioned in a VC on December 8th, a few days earlier. ↩
-
This is a relic of the unused 2 player mode logic, which is surprisingly complete considering how none of it appears in the actual game. ↩
